ΜΕΛΙΣΣΕΣ - ΚΡΥΦΑ

ΜΙΧΑΛΗΣ ΧΑΤΖΗΓΙΑΝΝΗΣ - ΤΟ ΚΑΛΟΚΑΙΡΙ ΜΟΥ

ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ Β' ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ

Για να δείτε ένα πλήρες βοήθημα πάνω στη φυσική Β' Λυκείου πατήστε εδώ .

ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ Α' ΛΥΚΕΙΟΥ

Για να δείτε ένα πλήρες βοήθημα πάνω στη Φυσική Α' Λυκείου πατήστε εδώ .

ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ Γ' ΓΥΜΝΑΣΙΟΥ

Για να δείτε ένα πλήρες βοήθημα πάνω στη Φυσική της Γ' Γυμνασίου πατήστε εδώ .

ΠΛΗΡΕΣ ΒΟΗΘΗΜΑ ΦΥΣΙΚΗΣ Β' ΓΥΜΝΑΣΙΟΥ

Για να δείτε ένα πλήρες βοήθημα πάνω στη Φυσική Β' Γυμνασίου πατήστε εδώ .

ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΑ 3

Για να δείτε το ψηφιακό βοήθημα του υπουργείου πάνω στην ενότητα 3 των μιγαδικών αριθμών πατήστε εδώ .

ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΑ 2

Για να δείτε το ψηφιακό βοήθημα του υπουργείου πάνω στην ενότητα 2 των μιγαδικών αριθμών πατήστε εδώ .

ΦΑΙΝΟΜΕΝΟ DOPPLER

Δείτε μια πολύ ωραία προσομοίωση πάνω στο φαινόμενο στην παρακάτω σελίδα .Πατήστε εδώ και εδώ .

ΕΝΟΤΗΤΑ 5 . ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ

Πατήστε παρακάτω για την 5η ενότητα από το υπουργείο .
Ενότητα 5: Σύνθεση ταλαντώσεων

ΕΝΟΤΗΤΑ 4 . ΕΞΑΝΑΓΚΑΣΜΕΝΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Πατήστε παρακάτω για την 4η ενότητα από το υπουργείο .
Ενότητα 4: Εξαναγκασμένες ταλαντώσεις

ΕΝΟΤΗΤΑ 3 . ΦΘΙΝΟΥΣΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Πατήστε παρακάτω για την 3η ενότητα του υπουργείου .
Ενότητα 3: Φθίνουσες ταλαντώσεις

ΕΝΟΤΗΤΑ 2 - ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ

Πατήστε παρακάτω για να δείτε την 2η ενότητα από το Υπουργείο .

Ενότητα 2: Ηλεκτρικές ταλαντώσεις

ΕΝΟΤΗΤΑ 1.2 Α.Α.Τ. ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ - ΑΡΧΙΚΗ ΦΑΣΗ - ΟΡΜΗ

Πατήστε παρακάτω για να δείτε την δεύτερη ενότητα από τα ψηφιακά βοηθήματα του υπουργείου .
Ενότητα 1.2: Απλή αρμονική ταλάντωση (Ενεργειακή προσέγγιση, Αρχική φάση, Σύστημα ελατηρίου σώματος, Ορμή)

ΕΝΤΑΣΗ - ΔΥΝΑΜΙΚΟ ΣΕ ΣΥΝΘΕΤΟ ΠΕΔΙΟ

Ενταση - Δυναμικό σύνθετου ηλεκτρικού πεδίου

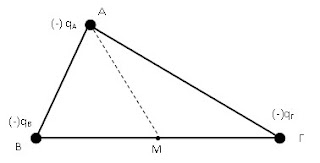
Στις κορυφές Α, Β και Γ τριγώνου ΑΒΓ πλευράς ΒΓ = 0,2m, συγκρατούνται ακίνητα τα σημειακά φορτία q_Α = -6 μC και q_Β = q_Γ = q = -2 μC .

Να υπολογίσετε:

α) Την ένταση του ηλεκτρικού πεδίου των τριών φορτίων, στο μέσο M της πλευράς ΒΓ, αν ΑΜ = 0,1m.

β) Το συνολικό δυναμικό του ηλεκτρικού πεδίου των τριών φορτίων, στο μέσο M της πλευράς ΒΓ.

γ) Το έργο της δύναμης του πεδίου για τη μετακίνηση ενός φορτίου q₃ = -3μC από το σημείο Μ στο άπειρο.

δ) Τη δυναμική ενέργεια που θα αποκτήσει το φορτίο q₃ = -3μC, όταν τοποθετηθεί στο σημείο Μ. Τι εκφράζει το πρόσημό της;

ε) Την κινητική ενέργεια με την οποία φτάνει το q₃ στο άπειρο, αν αφεθεί ελεύθερο στο σημείο Μ. Τι παρατηρείτε;

Δίνεται: k = 9·10⁹ Ν·m²/C²

Η συνέχεια ΕΔΩ

ΤΡΙΩΡΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ

Δείτε όλο το διαγώνισμα από εδώ.

ΜΙΑ ΙΔΙΟΜΟΡΦΗ ΤΑΛΑΝΤΩΣΗ

Μια ιδιόμορφη ταλάντωση

Υλικό σημείο Σ ενός ελαστικού μέσου εκτελεί περιοδική κίνηση (ιδιόμορφη ταλάντωση) της οποίας η εξίσωση απομάκρυνσης από τη θέση χ=0, εκφράζεται ως επαλληλία των εξισώσεων κίνησης:
χ1=0,1ημ(202πt) (S.I) και χ2=0,1ημ(198πt) (S.I)

α) Να γραφεί η εξίσωση κίνησης του Σ

β) Ποιες χρονικές στιγμές μηδενίζεται ο όρος της περιοδικής κίνησης που μεταβάλλεται αργά με το χρόνο (περιβάλλουσα); Ποια χρονική στιγμή μηδενίζεται για πρώτη φορά; Ποια η φάση των δύο εξισώσεων χ1 , χ2 από την επαλληλία των οποίων προκύπτει η εξίσωση κίνησης του Σ, ποια η διαφορά φάσης μεταξύ τους και ποιες οι τιμές των χ1 , χ2 και της απομάκρυνσης χ τη στιγμή αυτή;

γ) Ποιες χρονικές στιγμές γίνεται μέγιστος κατά απόλυτη τιμή ο όρος της περιοδικής κίνησης που μεταβάλλεται αργά με το χρόνο (περιβάλλουσα); Ποια χρονική στιγμή συμβαίνει αυτό για πρώτη φορά; Ποια η φάση των δύο εξισώσεων χ1 , χ2 από την επαλληλία των οποίων προκύπτει η εξίσωση κίνησης του Σ, ποια η διαφορά φάσης μεταξύ τους και ποιες οι τιμές των χ1 , χ2 και της απομάκρυνσης χ τη στιγμή αυτή;

δ) Πόσες πλήρεις ταλαντώσεις της περιοδικής κίνησης εκτελεί το υλικό σημείο σε χρονικό διάστημα ίσο με αυτό που μεσολαβεί μεταξύ δύο διαδοχικών μηδενισμών της περιβάλλουσας;

Για να δείτε την απάντηση πατήστε εδώ .

ΘΕΡΜΟΔΥΝΑΜΙΚΗ

1ος Θερμοδυναμικός νόμος σε μεταβολές αερίων.

Ένα αέριο εκτελεί την κυκλική μεταβολή του σχήματος, όπου Ρ_Α=4.10⁵ N/m², V_Α=20L και V_Β=40L.

Αν κατά την μεταβολή ΑΒ το αέριο προσλαμβάνει θερμότητα 15.000J, ενώ κατά την με ταβολή ΒΓ αποβάλλει θερμότητα 7.000J, να βρεθούν το έργο, η μεταβολή της εσωτερι κής ενέργειας και η θερμότητα που ανταλλάσσει το αέριο με το περιβάλλον στη μεταβολή ΓΑ.

Για να δείτε την απάντηση πατήστε εδώ .

ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ

Δύο ήχοι και μια σύνθεση.

Διαθέτουμε δύο ηχητικές πηγές που παράγουν απλούς αρμονικούς ήχους της ίδιας συχνότητας. Οι δυο πηγές παράγουν ήχους ίδιας έντασης, πράγμα που σημαίνει ότι, όταν ο κάθε ήχος πέσει στο τύμπανο του αυτιού μας, το εξαναγκάζει να ταλαντωθεί με το ίδιο πλάτος. Έστω ότι η ταλάντωση του τυμπάνου εξαιτίας του πρώτου ήχου έχει απομάκρυνση:

x₁=0,002 ημ(1000πt) (S.Ι.).

ενώ εξαιτίας του δεύτερου ήχου:

x₂=0,002∙ημ(1000πt+2π/3) (S.Ι.).

i) Ποια η συχνότητα του ήχου που ακούμε;

ii) Να βρεθεί η εξίσωση της απομάκρυνσης του τυμπάνου του αυτιού μας σε συνάρτηση με το χρόνο.

iii) Να βρείτε την ταχύτητα ταλάντωσης του τυμπάνου τη χρονική στιγμή t₁=1ms.

Για να δείτε την απάντηση πατήστε εδώ .

ΔΙΑΚΡΟΤΗΜΑ

Ταυτόχρονες ΑΑΤ και διακροτήματα

Υλικό σημείο Σ μάζας m=2∙10^-2kg εκτελεί “ταυτόχρονα” δύο AAT, οι οποίες γίνονται στην ίδια διεύθυνση, γύρω από την ίδια θέση ισορροπίας και με συχνότητες που διαφέρουν πολύ λίγο. Οι ταλαντώσεις περιγράφονται από τις εξισώσεις: x₁=Αημ(2πf₁t) και x₂=Αημ(2πf₂t), με f₁>f₂. Από τη σύνθεση των δύο ΑΑΤ προκύπτει μια ιδιόμορφη ταλάντωση του Σ που παρουσιάζει διακροτήματα. Η απομάκρυνση και το “πλάτος” της ιδιόμορφης ταλάντωσης του Σ σε σχέση με το χρόνο φαίνονται στο διάγραμμα.

Να βρεθούν:

α. Το πλάτος Α των δύο ΑΑΤ που δημιουργούν την ιδιόμορφη ταλάντωση.

β. Η περίοδος και η συχνότητα των διακροτημάτων.

γ. Η περίοδος και η συχνότητα της ιδιόμορφης ταλάντωσης του Σ.

δ. Οι συχνότητες των δύο ΑΑΤ που δημιουργούν την ιδιόμορφη ταλάντωση.

ε. Η διαφορά φάσης των δύο ΑΑΤ τις χρονικές στιγμές 5s και 10s.

στ. Η απομάκρυνση, η ταχύτητα και η κινητική ενέργεια του Σ, την χρονική στιγμή που το πλάτος της ιδιόμορφης περιοδικής κίνησής του ισούται με 1m.

ζ. Ο αριθμός των μεγιστοποιήσεων του πλάτους και ο αριθμός των μηδενισμών της απομάκρυνσης του Σ, στη χρονική διάρκεια 0 - 50s.

Για να δείτε την απάντηση πατήστε εδώ .

ΚΡΟΥΣΗ ΣΕ ΤΑΛΑΝΤΩΣΗ

Μια επαφή, που κινδυνεύει να χαθεί ... λόγω κρούσης.

Ένα ελατήριο, σταθεράς k = 100 N/m, είναι στερεωμένο στο κάτω άκρο του με τον άξονά του κατακόρυφο. Στο πάνω άκρο του βρίσκεται στερεωμένος ένας αβαρής οριζόντιος δίσκος και πάνω σ’ αυτόν είναι τοποθετημένο ένα σώμα μάζας m = 1,6 kgr, χωρίς να είναι στερεωμένο με το δίσκο. Το σύστημα βρίσκεται σε κατάσταση ισορροπίας. Από ύψος h = 20 cm, πάνω από το σώμα που στηρίζεται στο δίσκο, αφήνουμε χωρίς αρχική ταχύτητα ένα δεύτερο σώμα μάζας ίσης με το πρώτο, το οποίο συγκρούεται πλαστικά με αυτό και το συσσωμάτωμα που δημιουργείται αρχίζει να κάνει α.α.τ.

α) Να βρείτε την ενέργεια και το πλάτος της ταλάντωσης του συσσωματώματος.

β) Αν το ύψος είναι μεγαλύτερο κάποιου h_o, το συσσωμάτωμα σε κάποια θέση αποσπάται από τον αβαρή δίσκο. Ποια είναι η θέση αυτή;

γ) Υπολογίστε το h_o, ώστε το συσσωμάτωμα να συνεχίσει να εκτελεί την α.α.τ.

Δίνεται ότι g = 10 m/sec².

Για να δείτε την απάντηση πατήστε εδώ .

ΔΥΟ ΗΧΟΙ - ΕΝΑ ΔΙΑΚΡΟΤΗΜΑ

Δύο ήχοι και ένα διακρότημα.

Διαθέτουμε δύο ηχητικές πηγές που παράγουν απλούς αρμονικούς ήχους με συχνότητες f₁ και f₂. Οι δυο πηγές παράγουν ήχους ίδιας έντασης, πράγμα που σημαίνει ότι, όταν ο κάθε ήχος πέσει στο τύμπανο του αυτιού μας, το εξαναγκάζει να ταλαντωθεί με το ίδιο πλάτος. Έστω ότι η ταλάντωση του τυμπάνου εξαιτίας του πρώτου ήχου έχει απομάκρυνση:

x₁=0,002 ημ(20.000πt+π) (S.Ι.).

ενώ εξαιτίας του δεύτερου ήχου:

x₂=0,002∙ημ(20.004πt) (S.Ι.).

i) Να βρεθούν οι συχνότητες των δύο ήχων.

ii) Να βρεθεί η διαφορά φάσης Δφ₂₁= φ₂-φ₁ μεταξύ των δύο απομακρύνσεων σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση.

iii) Να βρεθεί η εξίσωση της απομάκρυνσης του τυμπάνου του αυτιού μας σε συνάρτηση με το χρόνο.

iv) Ποια η συχνότητα του ήχου που αντιλαμβανόμαστε;

v) Πόσα μέγιστα της έντασης του ήχου αντιλαμβανόμαστε σε κάθε δευτερόλεπτο;
Για να δείτε την απάντηση πατήστε εδώ .

ΤΑΛΑΝΤΩΣΗ - ΑΝΑΠΗΔΗΣΗ

Ταλάντωση - αναπήδηση

Αφήνω ταυτόχρονα και τα δυο σώματα να πέσουν. Το ελατήριο έχει το φυσικό του μήκος και το πράσινο σώμα ακινητοποιείται στο δάπεδο.

Από ποιο ύψος πρέπει να αφεθεί το σύστημα ώστε το πράσινο να αναπηδήσει ;






Για να δείτε την απάντηση πατήστε εδώ .

ΚΡΟΥΣΗ ΚΑΙ ΠΛΑΤΟΣ ΤΑΛΑΝΤΩΣΗΣ

Κρούση και πλάτος ταλάντωσης

Τα σώματα Σ₁ και Σ₂ έχουν ίσες μάζες m₁ = m₂ = m = 9kg, το δάπεδο είναι λείο και το Σ₂ είναι στερεωμένο σε ελατήριο σταθεράς k = 25∙π² N/m και ισορροπεί όπως φαίνεται στο σχήμα. Το Σ₁ κινείται με οριζόντια ταχύτητα υ = 3,14m/sec και συγκρούεται με το Σ₂. Να βρεθεί η μέγιστη συσπείρωση του ελατηρίου, αν τα δύο σώματα συγκρούονται ξανά μετά από: (α) Δt = 0,6sec (β) Δt = 0,5sec

Για να δείτε την απάντηση πατήστε εδώ .

ΤΑΛΑΝΤΩΣΗ ΣΕ ΑΣΑΝΣΕΡ

Μια ταλάντωση σε ασανσέρ

Ένας ανελκυστήρας μάζας Μ=200kg διαθέτει για λόγους ασφαλείας κατακόρυφη ανάρτηση που είναι προσαρμοσμένη στο κάτω μέρος του, όπως φαίνεται στο σχήμα Η ανάρτηση λειτουργεί ως ιδανικό ελατήριο σταθεράς Κ=25000Ν/m. Επιβαίνων μάζας m=50kg βρίσκεται εντός του ανελκυστήρα. Το σύστημα, λόγω ατέλειας, σταματά h=15cm πάνω από το έδαφος. Στη συνεχεία αποδεσμεύεται πλήρως και τη χρονική στιγμή t₀=0 προσκρούει στο έδαφος όπου το ελεύθερο άκρο του ελατηρίου στερεώνεται ακλόνητα. Ο επιβαίνων και ο ανελκυστήρας να θεωρηθούν σημειακά αντικείμενα. Όλες οι κινήσεις γίνονται σε κοινή κατακόρυφη διεύθυνση Αντίσταση αέρα δεν υπάρχει. Για τις πράξεις δίνονται: g=10m/s². ημ(π/6)=ημ(5π/6) = 0,5.

Α. Να υπολογίσετε τη μέγιστη συμπίεση του ελατηρίου. Θεωρείστε δεδομένο ότι ο επιβαίνων βρίσκεται συνεχώς σε επαφή με το δάπεδο του ανελκυστήρα.

Β. Να γράψετε την εξίσωση ταχύτητας του συστήματος και να υπολογίσετε τη χρονική στιγμή που το σύστημα ακινητοποιείται στιγμιαία για πρώτη φορά. Θεωρείστε τον θετικό κατακόρυφο ημιάξονα Οy προσανατολισμένο προς τα πάνω.

Γ. Να υπολογίσετε τη μέγιστη και την ελάχιστη κατά μέτρο δύναμη που δέχεται ο επιβαίνων από το δάπεδο του ανελκυστήρα.
Για να δείτε την απάντηση πατήστε εδώ .

ΜΙΑ ΑΛΛΗ ΕΡΜΗΝΕΙΑ ΤΩΝ ΕΞΑΝΑΓΚΑΣΜΕΝΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΤΟΥ ΣΥΝΤΟΝΙΣΜΟΥ

Kαμπύλη των εξαναγκασμένων ταλαντώσεων

Είμαστε σε γάμο.Ο καθηγητής είναι ο κλαριτζής που μπορεί να παίξει οποιοδήποτε
τραγούδι από τα πολύ αργά ( Fδιεγέρτη μικρή) μέχρι τα πολύ γρήγορα ποντιακά (Fδιεγέρτη
μεγάλη). Ταλαντωτής είναι ο μαθητής που έχει όμως ένα μόνο αγαπημένο τραγούδι
(ιδιοσυχνότητα του).Πότε ο μαθητής θα χορέψει με το περισσότερο κέφι;Φυσικά όταν ο
κλαριτζής (καθηγητής) του παίξει το αγαπημένο του τραγούδι (Fδιεγ=Fo).Φυσικά πάντα ο
μαθητής χορεύει ότι του παίζει ο κλαριτζής (Fταλ=Fδιεγέρτη) αλλά όχι φυσικά με την ίδια
διάθεση (Πλάτος)........

ΕΞΕΤΑΣΤΕΑ ΥΛΗ

H εξεταστέα– διδακτέα ύλη των Πανελλαδικώς εξεταζόμενων μαθημάτων της Γ΄ Τάξης Ημερησίων & Δ΄ Τάξης Εσπερινών ΕΠΑ.Λ. για το σχολικό έτος 2010-2011

Πατήστε εδώ .

ΜΕΤΑΒΟΛΗ ΧΩΡΗΤΙΚΟΤΗΤΑΣ ΠΥΚΝΩΤΗ

Μεταβολή χωρητικότητας πυκνωτή με σταθερό φορτίο

Οι οπλισμοί επίπεδου πυκνωτή είναι κυκλικοί δίσκοι με ακτίνα r=6cm, απέχουν l=1mm και στο χώρο μεταξύ τους υπάρχει διηλεκτρικό με ε=10.

Να υπολογίσετε τη χωρητικότητα του πυκνωτή.

Αν συνδέσουμε τον πυκνωτή με πηγή με τάση V=10V, πόσο φορτίο θα αποκτήσει, πόση θα είναι η ενέργειά του και πόση η ένταση του ομογενούς ηλεκτρικού πεδίου στο χώρο μεταξύ των οπλισμών του;

Αποσυνδέουμε τον πυκνωτή από την πηγή, που τον φόρτισε, και βγάζουμε το διηλεκτρικό, ενώ ταυτόχρονα διπλασιάζουμε την απόσταση των οπλισμών του. Να βρείτε τη χωρητικότητα, το φορτίο, την τάση, την ενέργεια και την ένταση του ομογενούς ηλεκτρικού πεδίου για τη νέα κατάσταση του πυκνωτή.

Δίνεται ε_ο=10^-9/36π C²/N×m².

Για να δείτε την απάντηση πατήστε εδώ .

ΜΕΤΑΒΟΛΗ ΧΩΡΗΤΙΚΟΤΗΤΑΣ ΠΥΚΝΩΤΗ

Μεταβολή χωρητικότητας πυκνωτή με σταθερή τάση

Επίπεδος πυκνωτής έχει χωρητικότητα C_o=1μF και είναι συνδεδεμένος με πηγή σταθερής τάσης V_o=20V.

Διατηρούμε τη σύνδεση με την πηγή, διπλασιάζουμε την απόσταση των οπλισμών του και γεμίζουμε το χώρο στο εσωτερικό του με διηλεκτρικό με ε=5.

Να βρείτε τη μεταβολή και την % μεταβολή της τάσης του, της χωρητικότητάς του, του φορτίου του και της ενέργειάς του.

Για να δείτε την απάντηση πατήστε εδώ .

ΕΝΕΡΓΕΙΑ ΓΙΑ ΤΗΝ ΑΠΟΜΑΚΡΥΝΣΗ ΟΠΛΙΣΜΩΝ ΠΥΚΝΩΤΗ

Ενέργεια για την απομάκρυνση οπλισμών πυκνωτή.

Ένας πυκνωτής με χωρητικότητα 2μF φορτίζεται με φορτίο 0,4mC και κατόπιν αποσυνδέουμε τη πηγή. Η απόσταση των οπλισμών του είναι 0,1mm. Θέλουμε να απομακρύνουμε τους οπλι­σμούς ώστε η απόσταση μεταξύ τους να γίνει 0,2mm. Επειδή οι οπλισμοί φέρουν αντίθετα φορτία έλκονται. Αυτό σημαίνει ότι πρέπει να τραβήξουμε τους οπλισμούς και απαιτείται έρ­γο.

Τι γίνεται το έργο αυτό;

Να υπολογίστε το έργο για την παραπάνω περίπτωση.


Για να δείτε την απάντηση πατήστε εδώ .

ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΠΑΝΩ ΣΤΟ ΝΟΜΟ ΤΟΥ ΚΟΥΛΟΜΠ ΚΑΙ ΤΗΝ ΕΝΤΑΣΗ

Για να δείτε το φύλλο εργασίας πατήστε εδώ .

ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΠΕΔΙΟΥ

Πόσο είναι τα φορτία;

Στις κορυφές Β και Γ ενός ισοσκελούς τριγώνου ΑΒΓ βρίσκονται δύο σημειακά φορτία q₁ και q₂ αντίστοιχα. Φέρνουμε ένα τρίτο σημειακό αρνητικό φορτίο –q στην κορυφή Α και παρατηρούμε ότι δέχεται δύναμη F παράλληλη προς την βάση ΒΓ, όπως στο σχήμα.

1. Να σχεδιάστε την ένταση του πεδίου στην κορυφή Α.
2. Ποια είναι τα πρόσημα των φορτίων q₁ και q₂;
3. Αν |q₁|= 1μC, πόσο είναι το φορτίο q₂;

Για να δείτε την απάντηση πατήστε εδώ .

ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΠΕΔΙΟΥ

Ένταση Ηλεκτρικού πεδίου και φορτίο πηγή.

Ένα σημειακό φορτίο q βρίσκεται σε μια από τις κορυφές Α, Γ, Δ ενός τετραγώνου ΑΒΓΔ πλευράς α. Η ένταση του πεδίου, που δημιουργεί το φορτίο, στην κορυφή Β φαίνεται στο σχήμα και έχει μέτρο Ε_Β=100Ν/m.

1. Σε ποια κορυφή βρίσκεται το φορτίο q;
2. Ποιο το πρόσημο του φορτίου;
3. Να σχεδιάστε την ένταση του πεδίου στο κέντρο Ο του τετραγώνου και να υπολογίστε το μέτρο της.

Για να δείτε την απάντηση πατήστε εδώ .

ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΠΕΔΙΟΥ

Υπολογισμός Έντασης Ηλεκτρικού πεδίου.

Στις κορυφές Β και Γ ισοπλεύρου τριγώνου ΑΒΓ πλευράς α=3cm βρίσκονται δύο σημειακά φορτία q₁= + 0,1μC και q₂ αντίστοιχα. Αν η ελκτική δύναμη που δέχεται το φορτίο q₂ από το φορτίο q₁ έχει μέτρο 0,1Ν, να βρεθεί η ένταση του ηλεκτρικού πεδίου που οφείλεται στα δύο φορτία:

1. Στο μέσον Μ της ΒΓ.
2. Στην κορυφή Α του τριγώνου.

Δίνεται k=9·10⁹Νm²/C².

Για να δείτε την απάντηση πατήστε εδώ .

ΦΟΡΤΙΟ ΚΑΙ ΜΑΖΑ ΗΛΕΚΤΡΟΝΙΟΥ

Μι­κρή σφαί­ρα έ­χει φορ­τί­ο -2μC.

1. Πό­ση δύ­να­μη ε­ξα­σκεί σε έ­να η­λε­κτρό­νιο που α­πέ­χει 1cm α­πό το κέ­ντρο της;
2. Πό­σα η­λε­κτρό­νια πρέ­πει να τις α­φαι­ρέ­σου­με για να αποφορτιστεί;
3. Πό­σο θα αλ­λά­ξει η μά­ζα της;
   e=-1,6·10^-19C, m_e=9,1·10^-31kg.

Για να δείτε την απάντηση πατήστε εδώ .

ΒΑΡΥΤΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΔΥΝΑΜΕΙΣ

Έχουμε έναν κρύσταλλο ΝaCl όπου τα ιόντα απέχουν απόσταση r=10^-8m.

1. Να υπολογίσετε τα μέτρα των δυνάμεων που ασκεί το ένα ιόν στο άλλο, εξαιτίας:
   ....Α) της βαρυτικής έλξης
   .....Β) της δύναμης Coulomb.
2. Να συγκρίνετε τα μέτρα των δυνάμεων και να σχολιάστε το αποτέλεσμα.

Δίνονται m_Na= 23m_p, m_Cl=35,5m_p, m_p=1,6·10^-27kg, q_p= - q_e= 1,6·10^-19C, G=6,67·10^-11Nm²/kg², K=9·10⁹Nm²/kg<sup>2

Για να δείτε την απάντηση πατήστε εδώ .</sup>

Τι συμβαίνει κατά την διάρκεια ενός κεραυνού ;

ΑΣΚΗΣΗ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ

Μια αντιλόπη τη στιγμή που αντιλαμβάνεται την παρουσία ενός λιονταριού σε απόσταση 70m απ’ αυτήν, ξεκινά να απομακρύνεται με σταθερή ταχύτητα 19m/s, ενώ ταυτόχρονα το λιοντάρι αρχίζει να την καταδιώκει με σταθερή ταχύτητα 20m/s.

Αν γνωρίζετε ότι τα ζώα μπορούν να κινούνται με σταθερή ταχύτητα, η μεν αντιλόπη το πολύ για χρόνο 60s, το δε λιοντάρι το πολύ για απόσταση 1000m, και στη συνέχεια σταματούν, λόγω κούρασης, να βρείτε αν γλίτωσε ή όχι η αντιλόπη.

Για να δείτε την απάντηση πατήστε εδώ .

ΠΥΚΝΩΤΗΣ

Στο παρακάτω σχήμα ο επίπεδος πυκνωτής χωρητικότητας C=1nF φορτίζεται από μια πηγή τάσης V=50V, οι οπλισμοί του απέχουν ℓ=1cm, ο διακόπτης δ₂ είναι κλειστός, ενώ ο δ₁ ανοικτός.

i) Πόσο είναι το φορτίο κάθε οπλισμού του πυκνωτή;

ii) Μπορείτε να βρείτε το δυναμικό του οπλισμού Α;

iii) Κλείνουμε το διακόπτη δ₁. Δίνεται ότι το δυναμικό της Γης είναι μηδέν, οπότε το σημείο Γ του κυκλώματος που «γειώνεται» αποκτά δυναμικό ίσο με μηδέν.

Χαρακτηρίστε ως σωστές ή λανθασμένες τις παρακάτω προτάσεις.

α) Το φορτίο του πυκνωτή θα αυξηθεί.

β) Θα φύγουν ηλεκτρόνια από τον οπλισμό Β και θα πάνε στη Γη.

γ) Η ενέργεια του πυκνωτή θα μειωθεί.

δ) Το δυναμικό του οπλισμού Α γίνεται ίσο με 50V.

iv) Ανοίγουμε τώρα τον διακόπτη δ₂. Πόσο γίνεται τώρα το δυναμικό του οπλισμού Α;

v) Φέρνουμε ένα σημειακό φορτίο q₁=1pC πολύ κοντά στον θετικό οπλισμό. Να βρείτε:

α) Τη δύναμη που δέχεται από το πεδίο.

β) Τη δυναμική ενέργεια του φορτίου q₁.

Για να δείτε την απάντηση πατήστε εδώ .

ΣΥΝΘΕΣΗ ΤΑΛΑΝΤΩΣΕΩΝ ΙΔΙΑΣ ΣΥΧΝΟΤΗΤΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ

Σώμα μάζας m=1kg εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις με ίσα πλάτη (A₁=A₂) και εξισώσεις x₁= A₁·ημωt και x₂= A₂ ημ(ωt+π/3) (S.I.), που εξελίσσονται πάνω στην ίδια ευθεία και γύρω από την ίδια θέση ισορροπίας ταλάντωσης. Η ενέργεια της σύνθετης κίνησης είναι Ε= 6 J και η μέγιστη επιτάχυνση που αποκτά είναι α_max= 20 √3 m/s²

α. Να βρείτε το πλάτος Α₁ και την γωνιακή συχνότητα ω της σύνθετης κίνησης.

β. Να γράψετε την εξίσωση της ταχύτητας σε συνάρτηση με τον χρόνο υ=υ(t) της σύνθετης κίνησης

γ. Να υπολογίσετε το μέτρο της ταχύτητας την χρονική στιγμή που ο ρυθμός μεταβολής της ορμής του σώματος είναι ίσος με ΔΡ/Δt= -10 √3 Κgm/sec².

δ. Να βρείτε την επιτάχυνση του σώματος, την χρονική στιγμή που η απομάκρυνσή του λόγω της 1^ης ταλάντωσης γίνεται ίση με x₁=0,1m, για πρώτη φορά μετά την έναρξη της σύνθετης κίνησης .

Για να δείτε την απάντηση πατήστε εδώ .

ΙΣΟΘΕΡΜΗ ΚΑΙ ΑΔΙΑΒΑΤΙΚΗ ΜΕΤΑΒΟΛΗ

Ένα αέριο βρίσκεται σε δοχείο που κλείνεται με έμβολο σε κατάσταση Α με πίεση p₁=32∙10⁵Ν/m².

i) Απορροφώντας θερμότητα Q₁=19.200ℓn2 J ισόθερμα, το αέριο έρχεται σε κατάσταση Β με πίεση p₂=4∙10⁵Ν/m². Να βρεθεί ο όγκος στην κατάσταση Α.

ii) Το ίδιο αέριο έρχεται από την κατάσταση Α σε κατάσταση Γ, σε πίεση p₃=1∙10⁵Ν/m² αδιαβατικά. Αν για το αέριο αυτό γ=5/3, ζητούνται:

α) Να βρεθεί ο όγκος V_Γ.

β) Το έργο κατά την αδιαβατική εκτόνωση.

γ) Να παρασταθούν στους ίδιους άξονες p-V οι μεταβολές ΑΒ και ΑΓ.

δ) Αν το αέριο μετέβαινε από την κατάσταση Β στην κατάσταση Γ αντιστρεπτά, ακολουθώντας τον «συντομότερο δρόμο», πόση θερμότητα θα αντάλλασσε το αέριο με το περιβάλλον του;

Για να δείτε την απάντηση πατήστε εδώ .