ΦΡΟΝΤΙΣΤΗΡΙΑ ΕΠΙΤΥΧΙΑ ΟΛΟΙ ΜΙΑ ΠΑΡΕΑ: Ιανουαρίου 2011

Δευτέρα 31 Ιανουαρίου 2011

Παρασκευή 28 Ιανουαρίου 2011

ΙΣΟΡΡΟΠΙΑ ΡΑΒΔΟΥ

Η ράβδος του σχήματος ισορροπεί οριζόντια δεμένη στο άκρο της με νήμα. Η δύναμη που δέχεται η ράβδος στο άκρο Α από την άρθρωση είναι:

α) Η F₁

β) η F₂

γ) η F₃

δ) η F₄

Εξηγείστε γιατί απορρίπτονται οι άλλες περιπτώσεις.

Απάντηση:

Η ράβδος του σχήματος έχει μήκος 4m και μάζα m=30kg, μπορεί να στρέφεται γύρω από οριζόντιο άξονα που περνά από το άκρο της Α, ενώ στηρίζεται σε κύλινδρο σε σημείο Μ, που απέχει 1m από το άκρο της Β. Ο συντελεστής τριβής μεταξύ σανίδας και κυλίνδρου είναι μ=0,2, ενώ η γωνία κλίσεως της ράβδου έχει ημθ=0,6. Ο κύλινδρος στρέφεται με σταθερή γωνιακή ταχύτητα ω=1rad/s, γύρω από τον άξονά του.

Να βρεθούν οι συνιστώσες της δύναμης που ασκείται από τον άξονα στη ράβδο, την F_x παράλληλη προς την ράβδο και F_y κάθετη σ’ αυτήν.
Πώς θα μεταβληθεί το μέτρο των παραπάνω συνιστωσών αν αυξήσουμε τη γωνιακή ταχύτητα στην τιμή ω₁=2rad/s;
Πώς θα μεταβληθεί το μέτρο των παραπάνω συνιστωσών αντιστραφεί η φορά περιστροφής του κυλίνδρου;

Απάντηση:

ΑΣΚΗΣΗ ΙΣΟΡΡΟΠΙΑΣ

Ισορροπία στερεού και δύναμη που ασκείται στη σανίδα από ένα κινούμενο σώμα.

Η ράβδος ΑΒ μήκους 4m και βάρους 100Ν μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Α και ισορροπεί όπως στο σχήμα, δεμένη με νήμα στο άκρο της Β, το οποίο είναι κάθετο σε αυτήν. Κατά μήκος της ράβδου κινείται ένα σώμα Σ μάζας m₁=5kg με επιτάχυνση α=2m/s². Αν η κλίση της σανίδας είναι θ, όπου ημθ=0,6 και συνθ = 0,8, να βρεθούν η τάση του νήματος και οι συνιστώσες της δύναμης που δέχεται η σανίδα από τον άξονα F_x και F_y, όπου η μια έχει την διεύθυνση της σανίδας και η άλλη κάθετη σε αυτήν τη στιγμή που το σώμα περνά από την θέση Ο, απέχοντας 1m από το άκρο B. g=10m/s².

Απάντηση:

ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ

Πάνω σε μια παγωμένη λίμνη ηρεμεί μια ομογενής σανίδα μήκους 4m. Σε μια στιγμή t=0 ένα κινούμενο υλικό σημείο Σ, συγκρούεται με τη σανίδα με αποτέλεσμα, αμέσως μετά την κρούση τα άκρα Α και Β της σανίδας να αποκτήσουν ταχύτητες υ_Α=20m/s και υ_Β=40m/s αντίστοιχα, όπως στο σχήμα (α).

α) Ποια η ταχύτητα του μέσου Ο της σανίδας.

β) Να βρεθεί η γωνιακή ταχύτητα περιστροφής της σανίδας, γύρω από το κέντρο μάζας της Ο.

γ) Σε πόσο χρόνο για πρώτη φορά η σανίδα θα βρεθεί στη θέση του σχήματος β;

δ) Για τη θέση (β):

	i) Ποιο είναι το άκρο Α και ποιο το Β;
	ii) Το άκρο Α ή το Β έχει μεγαλύτερη ταχύτητα;
	iii) Να βρεθεί η επιτάχυνση του κέντρου Ο και του άκρου Α της σανίδας.

Απάντηση

ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ

Κινηματική Στερεού. Κίνηση τροχού.

Στο σχήμα φαίνεται ο τροχός ενός αυτοκινήτου που κινείται με σταθερή ταχύτητα υ₀=10m/s σε οριζόντιο δρόμο. Το ανώτερο σημείο Α του τροχού έχει ταχύτητα υ₁=15m/s.

Ποιες προτάσεις είναι σωστές ή και ποιες λάθος:

Η μέγιστη γραμμική ταχύτητα ενός σημείου του τροχού είναι ίση με 5m/s.
Μεταξύ της ταχύτητας του αυτοκινήτου υ₀ και της γωνιακής ταχύτητας του τροχού ισχύει η σχέση υ₀=2ωR.
To σημείο επαφής του τροχού με το έδαφος (σημείο Β) έχει μηδενική ταχύτητα.
Ο τροχός του αυτοκινήτου σπινάρει.
Για την ταχύτητα του σημείου Γ, που βρίσκεται στο άκρο μιας οριζόντιας ακτίνας ισχύει υ_Γ²= 1,25 υ₀².
Δεν υπάρχει σημείο του τροχού με μηδενική ταχύτητα.
Το σημείο Α έχει μεγαλύτερη επιτάχυνση από το σημείο Β.

Απάντηση

ΣΤΡΟΦΙΚΗ - ΜΕΤΑΦΟΡΙΚΗ ΚΙΝΗΣΗ

Στα παρακάτω σχήματα φαίνονται δύο στερεά να κινούνται σε κυκλική τροχιά κέντρου Ο και ακτίνας R. Παρατηρώντας την κίνηση των σωμάτων, απαντήστε στις παρακάτω ερωτήσεις:

Στο σχήμα (α) το στερεό εκτελεί περιστροφική κίνηση.
Στο σχήμα (α) το στερεό εκτελεί μεταφορική κυκλική κίνηση.
Στο σχήμα (β) το στερεό εκτελεί περιστροφική κίνηση.
Στο σχήμα (β) το στερεό εκτελεί περιστροφική κίνηση.

Απάντηση:

ΚΥΛΙΣΗ ΣΩΜΑΤΟΣ

Ο τροχός ενός κάρου έχει μάζα Μ=10kg και ακτίνα R=0,8m, ενώ ένα σώμα Σ μάζας m₁=10kg, το οποίο θεωρείται υλικό σημείο, είναι προσδεδεμένο σε απόσταση r=0,6m από τον άξονα Ο του τροχού. Το κάρο κινείται με ταχύτητα υ=1,6m/s και ο τροχός κυλίεται χωρίς να ολισθαίνει.

Σε πόσο χρόνο ο τροχός ολοκληρώνει μια περιστροφή;
Ποια η μέγιστη και ποια η ελάχιστη ταχύτητα του σώματος Σ;
Ποια η υ_cm τη στιγμή που το σώμα Σ βρίσκεται στην κατακόρυφο που περνά από τον άξονα Ο του τροχού, όπως στο σχήμα;

Απάντηση:

ΕΡΩΤΗΣΗ ΘΕΩΡΙΑΣ

Κέντρο μάζας στερεού.

Να εξετασθεί η ορθότητα της πρότασης: «Αν το κέντρο μάζας ενός στερεού έχει ταχύτητα υ_cm, τότε το στερεό, εκτελεί μόνο μεταφορική ή σύνθετη κίνηση»

Απάντηση:

ΕΡΓΟ ΔΥΝΑΜΗΣ ΚΑΙ ΕΡΓΟ ΡΟΠΗΣ

Γύρω από έναν κύλινδρο ακτίνας R=0,4m, ο οποίος ηρεμεί σε λείο οριζόντιο επίπεδο, τυλίγουμε ένα αβαρές νήμα, στο άκρο Α του οποίου ασκούμε σταθερή οριζόντια δύναμη F=10Ν. Μετά από λίγο ο κύλινδρος έχει μετακινηθεί κατά x=16m, ενώ έχει περιστραφεί κατά γωνία θ=80rad.

α) Πόσο είναι το έργο της δύναμης F (σαν δύναμης).

β) Πόσο είναι το έργο της ροπής της δύναμης;

γ) Το συνολικό έργο της δύναμης είναι:

i) 160J,

ii) 320J,

iii) 480J.

δ) Το σημείο Α έχει μετακινηθεί κατά:

i) 16m,

ii) 32m,

iii) 48m.

ε) Να βρεθεί η μεταφορική και η περιστροφική κινητική ενέργεια του κυλίνδρου.

Απάντηση:

ΙΣΟΡΡΟΠΙΑ ΡΑΒΔΟΥ

ΙΣΟΡΡΟΠΙΑ ΡΑΒΔΟΥ ΚΑΙ ΡΟΠΕΣ

α) Η F₁

β) η F₂

γ) η F₃

δ) η F₄

Εξηγείστε γιατί απορρίπτονται οι άλλες περιπτώσεις.

Απάντηση:

ΛΑΜΠΤΗΡΑΣ

Πότε καίγεται ο λαμπτήρας.

.

Ο λαμπτήρας του σχήματος φωτοβολεί κανονικά με του διακόπτες ανοικτούς. Πότε υπάρχει κίνδυνος να καταστραφεί:

Όταν κλείσουμε τον διακόπτη Δ₁.
Όταν κλείσουμε τον διακόπτη Δ₂.
Όταν κλείσουμε και τους δύο διακόπτες.

Απάντηση:

ΝΟΜΟΣ ΤΟΥ OHM ΣΕ ΚΛΕΙΣΤΟ ΚΥΚΛΩΜΑ

Δίνεται το κύκλωμα, όπου R₁=R₂=10Ω, R₃=20Ω, ενώ η πηγή έχει ΗΕΔ Ε= 150V και εσωτερική αντίσταση r=2,5Ω. Ποια η ένδειξη του ιδανικού αμπερομέτρου με τον διακόπτη:

Ανοικτό
Κλειστό.

Απαντήσεις:

ΦΩΤΟΒΟΛΙΑ ΛΑΜΠΤΗΡΩΝ

Οι λαμπτήρες Α, Β, Γ και Δ του σχήματος είναι όμοιοι.

Αν ο λαμπτήρας Γ λειτουργεί κανονικά, ποιος κινδυνεύει να καεί, ο Α ή ο Δ;
Αν ο Δ λειτουργεί κανονικά:
i) θα λειτουργεί κανονικά και ο λαμπτήρας Γ ή όχι;
ii) Ποιος λαμπτήρας από τους άλλους τρεις φωτοβολεί περισσότερο;
Αν ξεβιδωθεί ο λαμπτήρας Β, τι θα συμβεί με την φωτοβολία των υπολοίπων;

Απάντηση:

ΜΕΓΙΣΤΗ ΙΣΧΥΣ

Δίνεται το τμήμα αβ ενός κυκλώματος, όπου R=5Ω. Αν η μέγιστη επιτρεπόμενη ισχύς για κάθε λαμπτήρα ξεχωριστά είναι 45W, να βρεθεί η μέγιστη ισχύς που μπορεί να καταναλωθεί στο τμήμα αβ.

Απάντηση:

ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ

Οι λάμπες στο παραπάνω κύκλωμα είναι ίδιες.
Να χαρακτηρίστε τις παρακάτω προτάσεις ως σωστές ή λαθεμένες.

Μόλις κλείσουμε τον διακόπτη δ, θα ανάψει πρώτη η λάμπα Λ₁.
Οι δυο λάμπες θα φωτοβολήσουν το ίδιο.
Αν μεταφέρουμε την Λ₁ στη θέση που φαίνεται στο παρακάτω κύκλωμα, τότε θα διαρρέεται από ρεύμα μικρότερης έντασης και θα φωτοβολεί λιγότερο.

.
Απαντηση:

ΚΑΝΟΝΕΣ KIRCHHOFF

Ποιες από τις παρακάτω προτάσεις που αναφέρονται στο κύκλωμα του σχήματος είναι σωστές:

i) Ι₁ > Ι₂.

ii) V_Α=V_Β.

iii) V_ΑΖ= V_ΒΓ+V_ΓΔ.

iv) V_ΒΓ+V_ΓΔ+V_ΔΖ+V_ΖΑ+V_ΑΒ=0

v) V_Γ > V_Δ.

Απάντηση:

ΦΟΡΑ ΚΑΙ ΤΙΜΗ ΤΗΣ ΕΝΤΑΣΗΣ ΤΟΥ ΡΕΥΜΑΤΟΣ

Ο κυλινδρικός αγωγός του σχήματος στενεύει στην περιοχή Β, ενώ στις περιοχές Α και Γ έχει την ίδια διατομή. Η ρευματική ταχύτητα των ελευθέρων ηλεκτρονίων του έχει φορά από το Α προς το Γ.

i) Η φορά του ηλεκτρικού ρεύματος είναι

α. από το Α προς το Γ. ............ β. από το Γ προς το Α.

ii) Για την ένταση του ρεύματος ισχύει

α. Ι_Α= Ι_Β= Ι_Γ ............β. Ι_Α> Ι_Β> Ι_Γ

γ. Ι_Α< Ι_Β< Ι _Γ δ. Ι_Α= Ι_Γ< Ι_Β

Απάντηση:

ΣΥΝΔΕΣΗ ΑΝΤΙΣΤΑΤΩΝ

Πόση είναι η συνολική αντίσταση μεταξύ των σημείων Α και Β;

Απάντηση:

ΝΟΜΟΣ ΤΟΥ OHM ΚΑΙ 1ος ΚΑΝΟΝΑΣ KIRCHHOFF

Στο τμήμα του κυκλώματος που φαίνεται στο σχήμα δίνονται R₂=20Ω, R₃=15Ω. Το ρεύμα που διαρρέει την R₂είναι 0,3Α, ενώ το αμπερόμετρο δείχνει 0,8Α.

Ποια η R₁;

Απάντηση:

ΣΥΝΕΧΕΣ ΡΕΥΜΑ - ΠΥΚΝΩΤΗΣ

Για το παρακάτω κύκλωμα δίνονται R₁=5Ω, R₂=3Ω, C=5μF, ενώ η πηγή έχει ΗΕΔ Ε=50V και εσωτερική αντίσταση r=2Ω και ο διακόπτης δ είναι κλειστός.

Ποια η ένταση του ρεύματος που διαρρέει το κύκλωμα και πόσο φορτίο είναι αποθηκευμένο στον πυκνωτή;
Σε μια στιγμή ανοίγουμε τον διακόπτη. Πόση θερμότητα θα παραχθεί στη συνέχεια πάνω στον αντιστάτη R₁;
Αν ο πυκνωτής είχε συνδεθεί στα άκρα των αντιστατών R₁,R₂, όπως στο παρακάτω σχήμα, πόση θερμότητα θα παραχθεί πάνω στον αντιστάτη R₁ μετά το άνοιγμα του διακόπτη δ;

Απάντηση:

Σάββατο 22 Ιανουαρίου 2011

ΚΙΝΗΣΗ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ

Κίνηση σε ομογενές Ηλεκτρικό πεδίο.

Ένα σωματίδιο με φορτίο q=-1nC και μάζα m=10^-10kg, κινείται παράλληλα προς τις δυναμικές γραμμές του ομογενούς ηλεκτρικού πεδίου του σχήματος, παράλληλα προς τις δυναμικές γραμμές και σε μια στιγμή (t₀=0) περνάει από το σημείο Α με ταχύτητα υ₀=40m/s.

Μετά από χρόνο 0,8ms το σωματίδιο περνά από το σημείο Β με ταχύτητα 120m/s.

Δίνεται ότι η απόσταση των δύο πλακών είναι ίση με d=0,1m, το σημείο Α απέχει 0,8cm από την αριστερή πλάκα Δ, ενώ το βάρος του σωματιδίου θεωρείται αμελητέο.

i) Υπολογίστε τη δύναμη που δέχεται το σωματίδιο από το πεδίο και την απόσταση (ΑΒ).

ii) Να βρεθεί η τάση V καθώς και η δυναμική ενέργεια του σωματιδίου στις θέσεις Α και Β.

iii) Να υπολογίσετε τη μεταβολή της κινητικής ενέργειας του σωματιδίου μεταξύ των δύο παραπάνω θέσεων και να τη συγκρίνετε με τις τιμές της δυναμικής ενέργειας του ii) ερωτήματος.

Απάντηση:

ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΚΥΜΑ

Ηλεκτρομαγνητικό κύμα και διάθλαση.

Δίνονται οι εξισώσεις για την ένταση ενός ηλεκτρικού και ενός μαγνητικού πεδίου, τα οποία μεταβάλλονται σε κάθετα επίπεδα

Ε= 120∙ημ 2π(αt-2∙10⁶x) και Β= 4∙10^-7∙ ημ 2π(αt-2∙10⁶x) (μονάδες στο S.Ι.)

i) Μπορούν οι παραπάνω εξισώσεις να περιγράφουν ένα ηλεκτρομαγνητικό κύμα που να διαδίδεται στο κενό;

ii) Αν πράγματι υπάρχει τέτοιο ηλεκτρομαγνητικό κύμα, να βρεθεί ο συντελεστής α του χρόνου, στην παραπάνω εξίσωση. Σε ποια περιοχή του φάσματος ανήκει αυτό το ΗΜΚ;

iii) Το παραπάνω κύμα προσπίπτει από τον αέρα σε πλάκα πάχους d=√2m, όπως στο σχήμα όπου θ=30°, οπότε φτάνει στο σημείο Β, σε απόσταση x=0,5m από το σημείο Α.

a) Να βρεθεί ο δείκτης διάθλασης του υλικού της πλάκας για το παραπάνω κύμα.

b) Αν η φάση του διαθλώμενου κύματος είναι της μορφής φ=ωt-kx΄, να προσδιορίσετε τις τιμές των ω και k.

Δίνεται c-3∙10⁸ m/s

Απάντηση:

Παρασκευή 21 Ιανουαρίου 2011

ΑΝΑΛΥΣΗ - ΣΥΝΘΕΣΗ ΔΥΝΑΜΕΩΝ

Ανάλυση – Σύνθεση δυνάμεων.

Σε ένα σώμα μάζας 6,5kg το οποίο ηρεμεί σε λείο οριζόντιο επίπεδο, κάποια στιγμή t₀=0, ασκούνται τρεις οριζόντιες δυνάμεις με μέτρα F₁=7Ν, F₂=10√2Ν και F₃=5Ν, όπως στο σχήμα, όπου φ=45°, ενώ για τη γωνία θ, ημθ=0,6 και συνθ=0,8.

i) Να αναλύσετε τις δυνάμεις πάνω στους δύο κάθετους άξονες x και y του σχήματος.

ii) Να βρείτε τη συνισταμένη των δυνάμεων σε κάθε άξονα.

iii) Να βρεθεί η συνισταμένη των τριών δυνάμεων.

iv) Να υπολογιστεί η ταχύτητα του σώματος τη στιγμή t=4s.

Απάντηση:

3ος ΝΟΜΟΣ ΝΕΥΤΩΝΑ

Τρίτος νόμος του Νεύτωνα, αντίδραση επιπέδου. Φύλλο εργασίας.

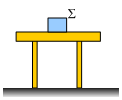
Ένα σώμα βάρους 20Ν ηρεμεί πάνω σε ένα τραπέζι, όπως στο σχήμα.

i) Σχεδιάστε τις δυνάμεις που ασκούνται πάνω του.

ii) Να υπολογιστούν τα μέτρα των δυνάμεων.

iii) Δυνάμεις από επαφή είναι …………… ενώ από απόσταση ……………….

iv) Ασκεί δύναμη το σώμα Σ στο τραπέζι; Αν ναι γιατί;

..........

Δείτε όλο το φύλλο εργασίας από εδώ.

ΚΑΤΑΚΟΡΥΦΗ ΒΟΛΗ - ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ

Ελεύθερη πτώση-Κατακόρυφη βολή. Ένα test.

1) Από το έδαφος εκτοξεύεται κατακόρυφα ένα σώμα με αρχική ταχύτητα υ₀=20m/s. Πάρτε έναν κατακόρυφο άξονα yy΄, θέστε το μηδέν στο έδαφος και θετική φορά προς τα πάνω.

Δίνεται η επιτάχυνση της βαρύτητας g=10m/s², ενώ η αντίσταση του αέρα θεωρείται αμελητέα.

i) Για την κίνηση του σώματος ισχύουν οι εξισώσεις:

υ= …………………… και y= ……………………………….

ii) Να βρεθεί η ταχύτητα και η θέση του σώματος τις χρονικές στιγμές:

α) t₁=1s και β) t₂=3s

iii) Μετά πόσο χρόνο και με ποια ταχύτητα επιστρέφει στο έδαφος;

iv) Στο παρακάτω σχήμα φαίνεται το σώμα σε τρεις θέσεις. Η Α θέση κατά την άνοδο, η Β όταν το σώμα βρίσκεται στο μέγιστο ύψος, ενώ στη θέση Γ, το σώμα κατεβαίνει. Και στις τρεις αυτές θέσει να σχεδιάστε την επιτάχυνση και την ταχύτητα του σώματος.

Μονάδες 10+40+20+30=100

2) Από το μπαλκόνι μιας πολυκατοικίας εκτοξεύεται για t=0, κατακόρυφα προς τα πάνω ένα σώμα με αρχική ταχύτητα υ₀=10m/s. Πάρτε έναν κατακόρυφο άξονα yy΄, θέστε το μηδέν στο σημείο εκτόξευσης και θετική φορά προς τα πάνω.

Δίνεται η επιτάχυνση της βαρύτητας g=10m/s², ενώ η αντίσταση του αέρα θεωρείται αμελητέα.

i) Για την κίνηση του σώματος ισχύουν οι εξισώσεις:

υ= …………………… και y= ……………………………….

ii) Να βρεθεί σε πόσο χρόνο το σώμα θα σταματήσει να κινείται προς τα πάνω και το μέγιστο ύψος από το σημείο εκτόξευσης, στο οποίο θα φτάσει.

iii) Αν το σώμα φτάνει στο έδαφος τη χρονική στιγμή t₁=3s, να βρεθούν:

α) Η ταχύτητα με την οποία το σώμα φτάνει στο έδαφος.

β) Το ύψος από το έδαφος του μπαλκονιού από το οποίο έγινε η εκτόξευση;

Μονάδες 10+40+20+30=100

ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΡΑΒΔΟΥ

Σύνθετη κίνηση ράβδου.

Μια ομογενής ράβδος μήκους ℓ=48/5π m≈3 m εκτοξεύεται από το έδαφος κατακόρυφα προς τα πάνω και φτάνει σε ύψος Η. Στο σχήμα, η πάνω θέση της ράβδου θέση (1), αντιστοιχεί στο μέγιστο ύψος, ενώ μετά από λίγο η ράβδος φτάνει στη θέση (2) έχοντας στραφεί κατά γωνία θ=π/3, έχοντας κατέλθει κατά h=0,8m.